De volgende theorie heeft betrekking op de wijze waarop 3D-graphics berekend worden. Welke processen spelen zich buiten het zicht van de gebruiker af in de computer?
Voor het genereren van computer graphics zijn veel en vaak complexe berekeningen nodig. Een gemiddeld boek over computer graphics staat stijf van de moeilijke formules, die voor de gemiddelde mens niet of nauwelijks te lezen zijn en niet echt uitnodigen om er mee aan de slag te gaan. In deze beknopte handleiding wordt de basis uitgelegd; hoe weet je computer welke kleur een bepaalde pixel heeft, welke delen van een voorwerp zichtbaar zijn, welke niet, et cetera. Met een minimum aan wiskunde.
Houd er rekening mee dat alle complexe theorieën en berekeningen niet voor niets bestaan. Als algemene regel geldt dat hoe hoger de kwaliteit van je 3D-graphics is, hoe complexer de berekeningen worden. Rendertijd kan dramatisch gereduceerd worden met complexe berekeningen. De basis is echter vrij eenvoudig en zijn tientallen jaren geleden al bedacht.
De besproken theorie is een zeer beperkte keuze uit het brede aanbod aan mogelijkheden en geeft een inzicht in hoe je zelf 3D-graphics kunt berekenen of hoe ze berekend worden door je 3D-programma.
Basis
Om een 3D-graphic te genereren heb je twee zaken nodig: één of meer virtuele voorwerpen, en een zogenaamd belichtingsmodel. Virtuele voorwerpen bestaan in het algemeen uit polygonen, of vlakken. Het belichtingsmodel beschrijft de manier waarop de virtuele voorwerpen reageren op virtueel licht. Wanneer het eindresultaat fotorealistisch moet zijn, wordt een belichtingsmodel gebruikt dat de fysieke wereld om ons heen zo dicht mogelijk benadert.
Polygonen
Virtuele voorwerpen worden in veel gevallen beschreven met behulp van polygonen. Eén enkele polygoon is op zich niet zo interessant. Meerdere polygonen kunnen een virtueel voorwerp representeren, bijvoorbeeld het logo van Fronteers.
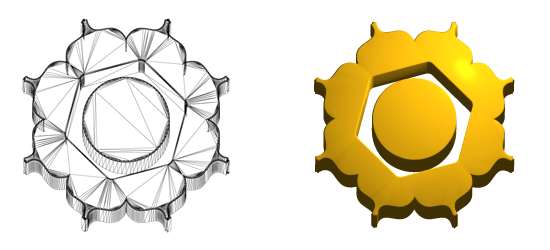
Polygonen zijn oppervlakken die begrensd worden door drie posities of hoekpunten in de ruimte met een x-, y- en z-positie. Polygonen die begrensd worden door drie hoekpunten hebben als voordeel dat ze altijd vlak zijn; je kunt de hoekpunten nooit zo in de virtuele ruimte plaatsen dat de polygoon niet vlak is. Naast polygonen met drie hoekpunten kun je ook polygonen met meer hoekpunten gebruiken, zolang het oppervlak vlak is.
Het is belangrijk dat een polygoon vlak is, omdat de geometrie van de polygoon gebruikt wordt in een aantal processen die gebaseerd zijn op vlakke polygonen. Veel software en hardware is geoptimaliseerd voor het verwerken van polygonen met drie hoekpunten.
De drie hoekpunten van een polygoon worden gebruikt om de ruimte die deze drie posities omsluiten als oppervlak te tonen. Elke positie binnen het oppervlak bestaat uit een x-, y- en z-positie die afgeleid kunnen worden van de drie hoekpunten. De posities zijn belangrijk, omdat deze gebruikt worden om te kijken of het wel of niet zichtbaar is. Wanneer er meerdere polygonen gebruikt worden kan een polygoon de andere overlappen. De positie wordt ook gebruikt om te berekenen welke kleur gebruikt moet worden en of de positie eventueel schaduw heeft.
In veel gevallen wordt een afbeelding gegenereerd. De afbeelding kan een enkele afbeelding zijn of een afbeelding uit een reeks die samen een animatie vormt. In het geval van een spelletje worden de afbeeldingen realtime op je scherm getoond, die net als een afbeelding ook uit pixels bestaat.
Er zijn twee typen afbeeldingen: raster graphics en vector graphics. Vector graphics beschrijven het beeld met behulp van wiskundige curves. Raster graphics of bitmap afbeeldingen bestaan uit puntjes of pixels. Elke pixel heeft een bepaalde kleur, die tezamen het beeld vormen.
Een bitmap afbeelding heeft een bepaald formaat in pixels, bijvoorbeeld 300 pixels horizontaal en 200 pixels verticaal; de afbeelding bestaat uit 60.000 pixels.
Hoe vertaal je een polygoon naar een afbeelding?
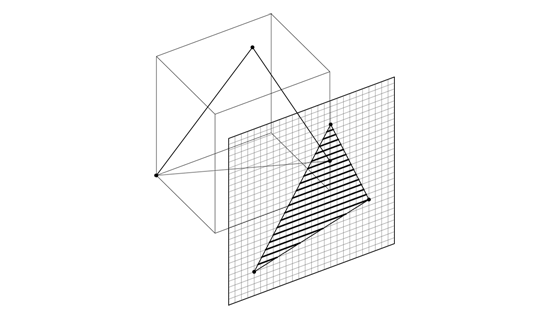
De posities van de hoekpunten van de polygoon zijn bekend, waardoor de minimum y-positie en maximale y-positie berekend kunnen worden. Eén van de hoekpunten van de polygoon is de minimum y-positie, een andere hoekpunt is de maximum y-positie van de polygoon. Het hoekpunt dat niet het verticale maximum of minimum is, bevindt zich tussen de minimum- en maximum y-positie.
Door de polygoon verticaal van boven naar beneden in horizontale lijnen te scannen kan de polygoon vertaald worden naar een afbeelding.
Het vertalen van een polygoon naar pixels wordt scanconversie of rasterization genoemd.
De horizontale start- en eindposities worden naar een pixelpositie vertaald. Deze horizontale startpositie heeft een x-, y- en z-positie, net als de eindpositie. Deze waarden zijn afgeleid van de drie hoekpuntposities van de polygoon.
Vervolgens worden alle posities die zich tussen de horizontale start- en eindpositie bevinden berekend.
Hoe meer polygonen gebruikt worden, hoe preciezer een virtueel voorwerp beschreven kan worden. Meer polygonen betekent ook dat er meer berekeningen nodig zijn.
Net als bij het gebruik van afbeeldingen op een website geldt; hoe hoger de kwaliteit, in veel gevallen hoe realistischer het eindresultaat moet worden, hoe langer het duurt voor de afbeelding geladen is, en in het geval van 3D-graphics hoe langer de rendertijd is.
Wanneer er meerdere polygonen gebruikt worden, is het van belang te weten welke (delen van) polygonen zichtbaar zijn voor de virtuele camera. Het volstaat niet om de polygonen een voor een te renderen.
Wanneer de virtuele camera om een virtueel voorwerp gedraaid wordt, is de ene keer de voorkant zichtbaar en de achterkant niet, deze bevindt zich achter de zichtbare voorkant. Wordt de camera verplaatst dan kan de achterzijde zichtbaar zijn en bevindt de voorkant zich achter de zichtbare achterzijde. Individuele polygonen zijn wel of niet of gedeeltelijk zichtbaar afhankelijk van de positie van de virtuele camera.
Voor het renderen van een virtuele omgeving is het dus noodzakelijk te kijken welke polygonen zichtbaar zijn en welke niet. De polygonen die zich het dichtst bij de camera bevinden zijn zichtbaar en overlappen mogelijk polygonen die verder van de camera verwijderd zijn. De afstand tot de camera wordt gebruikt om te bepalen welke (delen van de) polygonen wel of niet zichtbaar zijn. De afstand tot de camera wordt uitgedrukt als een z-waarde.
Per pixel moet uitgerekend worden welke positie van een polygoon zichtbaar is. Voor elke pixel wordt een stuk geheugen gereserveerd die de z-positie per pixel bijhoudt. Wanneer de z-positie van een polygon lager is dan de waarde in het geheugen (de z-buffer genoemd) wordt deze nieuwe waarde als minimum opgeslagen, met een verwijzing naar de polygoon waar de z-positie aan gerelateerd is.
Je kunt de z-buffer als afbeelding wegschrijven; dit levert een zogenaamde depth image op. Pixels met een hoge intensiteit hebben een lage z-waarde, pixels met een lage intensiteit hebben een hoge z-waarde.
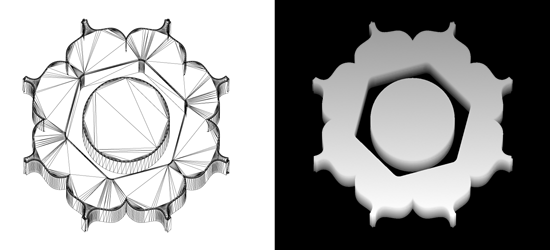
Polygonen die zich achter de camera bevinden, hebben een negatieve waarde en worden niet gebruikt, omdat je geen beeld kan zien dat zich achter de camera bevindt.
Belichtingsmodel
Om een voorwerp te kunnen zien is het noodzakelijk dat er een vorm van licht is. Licht wordt gereflecteerd door een voorwerp en de weerkaatsing van het licht valt op je netvlies waardoor je het voorwerp ziet.
Per pixel is na scanconversie duidelijk welke x-, y- en z-positie deze heeft. Naast de z-positie wordt bijgehouden bij welke polygoon de z-positie hoort. Met behulp van deze gegevens kan de kleur bepaald worden.
Voor het zichbaar maken van virtuele voorwerpen zijn een of meer virtuele lichten nodig.
Om de kleur van een pixel te bepalen kan virtueel licht opgedeeld worden in een aantal componenten: ambient, diffuus licht en specular, ook wel hooglicht genoemd. Door de intensiteit van deze drie componenten te combineren kan plastic, staal, et cetera nagebootst worden.
Ambient is licht gereflecteerd door alle voorwerpen in een omgeving. Diffuus licht wordt gereflecteerd door het oppervlak van een voorwerp. Afhankelijk van het materiaal waaruit het voorwerp bestaat, wordt licht in meer of mindere mate verstrooid gereflecteerd. Specular of hooglicht ontstaat wanneer een gereflecteerde lichtstraal het oog van de toeschouwer treft. Afhankelijk van de eigenschappen van een voorwerp zal hooglicht wel of niet zichtbaar zijn. Vilt reflecteert licht in vele richtingen, waardoor het licht verstrooid wordt en er niet of nauwelijks hooglicht zichtbaar is. Metaal heeft een vrij dicht en egaal oppervlak, waardoor licht minder verstrooid wordt en hooglicht zichbaar is als de gereflecteerde lichtstralen het oog treffen.
De intensiteit van diffuus licht wordt bepaald door de hoek tussen de lichtbron en de normaal van een polygoon te berekenen. De normaal van een polygoon staat loodrecht op het oppervlak van de polygoon en kan eenvoudig berekend worden met behulp van de drie hoekpunten van de polygoon.
De intensiteit van specular wordt bepaald door de hoek tussen de op het oppervlak gereflecteerde lichtstraal en het oog van de toeschouwer te berekenen. De gereflecteerde lichtstraal wordt berekend met behulp van de positie van de lichtbron en de normaal op het oppervlak van de polygoon. De hoek van inval is gelijk aan die van uitval.
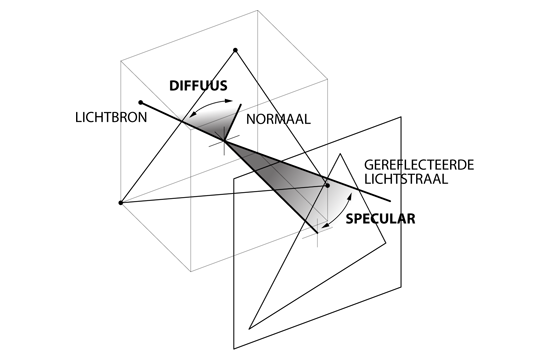
Het belichtingsmodel beschrijft de manier waarop de virtuele voorwerpen reageren op virtueel licht en bepaalt hoe de virtuele voorwerpen eruit komen te zien. Er bestaan vele belichtingsmodellen. De meest basale belichtingsmodellen zijn flat shading, Gouraud shading en Phong shading.
Flat shading is het meest eenvoudige belichtingsmodel. Voor elke polygoon wordt één enkele intensiteit berekend. Alleen de intensiteit van ambient en diffuus licht wordt gebruikt.
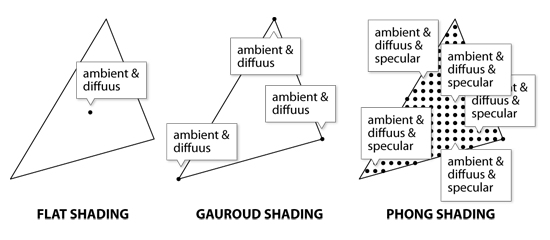
Gouraud shading is iets complexer. Voor elk hoekpunt van de polygoon wordt de intensiteit van ambient en diffuus licht gebruikt. De polygoon wordt vervolgens ingevuld met deze intensiteit. De drie berekende intensiteiten van de hoekpunten vloeien binnen het oppervlak van de polygoon in elkaar over.
Phong shading is complexer en rekenintensiever dan de voorgangers. Per positie wordt een intensiteit berekend. De intensiteiten van ambient, diffuus en specular worden gecombineerd. De normalen van de hoekpunten van de polygoon worden bij Phong shading gemiddeld met de normalen van aangrenzende polygonen die hetzelfde hoekpunt delen.
De berekende intensiteit wordt gecombineerd met de kleur-waarde van een polygoon en resulteert in de kleur van een pixel.
Kwaliteit
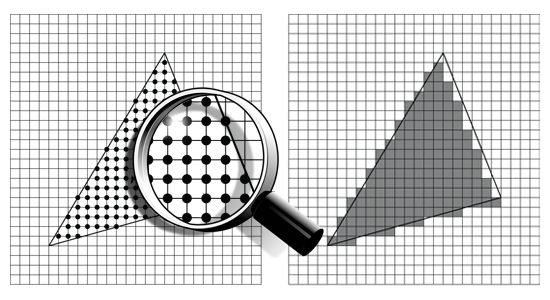
Nu bekend is hoe je een virtueel voorwerp zichtbaar kunt maken in de vorm van een afbeelding is de kwaliteit een aandachtspunt. Afhankelijk van de kwaliteit van de gebruikte virtuele voorwerpen kunnen lelijke trapjes, die ook wel jagged edges genoemd worden, ontstaan.
Je kunt dit probleem oplossen door de afbeelding op het dubbele formaat van het gewenste formaat te renderen en vervolgens de afbeelding in Photoshop, of een ander beeldverwerkingsprogramma, te schalen naar het gewenste formaat.
Het menselijke oog is gevoelig voor contrast. Wanneer het contrast vrij laag is, vloeien de kleuren van de pixels probleemloos in elkaar over. Daar waar veel contrast is, zullen de jagged edges storend zichtbaar zijn.
Door een filter—edge detection—op de afbeelding los te laten, kan de afbeelding omgezet worden naar een afbeelding waarbij de pixels met hoog contrast zichtbaar worden.
De intensiteit van pixels met een hoog contrast wordt herberekend. Door niet één positie per pixel te berekenen, maar vier of meer en vervolgens de kleurwaarden te middelen, kunnen de trapjes vermeden worden.
De techniek om jagged edges te vermijden wordt anti-aliasing genoemd.
Conclusie
3D-graphics zijn overal aanwezig: in films, in spelletjes, in reclame, enz. De basale kennis die je zojuist hebt opgedaan, geeft je een beter inzicht in de manier waarop de beelden tot stand komen. Het zelf maken van 3D-graphics is minder ingewikkeld dan je in eerste instantie misschien zou verwachten. Naarmate kwaliteit, realisme en snelheid belangrijker worden, neemt de complexiteit snel toe.
Zelfs als websitebouwer kun je wat aan 3D-graphicskennis hebben. Probeer je website na te bouwen in een 3D-programma. Als blijkt dat je website niet reproduceerbaar is—je kunt de schaduwen bijvoorbeeld niet namaken—dan is er iets mis met je ontwerp.
Links
Boeken
Advanced Animation and Rendering Techniques Alan Watt, M. Watt, ADDISON-WESLEY, ISBN 0-201-54412-1
Computer Graphics: Principles and Practice in C James D. Foley, Andries van Dam, Steven K. Feiner, John F. Hughes, ADDISON-WESLEY, ISBN 0-201-84840-6
Fundamentals of three-dimensional computer graphics Alan Watt, ADDISON-WESLEY, ISBN 0-201-15442-0
Over Arjan Westerdiep
Arjan Westerdiep is gediplomeerd kunstenaar, woordblind en probeert met wisselend succes zowel zijn linker als rechter hersenhelft te gebruiken en te combineren, was weer welkom op de lagere school zodra hij het telefoonnummer van zijn ouderlijk huis wist te onthouden, vindt iets mooi of lelijk en is de maker van [drububu.com](http://www.drububu.com).
Donatie: Leger des Heils Het Leger des Heils bekommert zich om degenen die niet de middelen, mogelijkheden en luxe hebben zich met zaken als anti-aliasing en z-buffers bezig te houden, omdat het ze ontbeert aan de meest basale middelen om een menswaardig leven te leiden en doen dat zonder enige vorm van discriminatie.